Numerical Integrals

01 Mar, 2024

A somewhat interesting topic is removed from the CAIE syllabus of 9709: Numerical Integration. Well, we still have the oldie but goodie trapezium rules:

\int_{a}^{b} f (x) d x = \frac{1}{2} (1 f (a) + 1 f (b)),

but this is hardly inspiring at all.

Interpolation with Equal Division

In Edexcel iAL syllabus, a more accurate Newton-Cotez formula is introduced, the 1/3 Simpson's rule:

\int_{a}^{b} f (x) d x = \frac{1}{6} (1 f (a) + 4 f (\frac{a + b}{2}) + f (b)) .

That is, by evaluating an additional point in the interval (the midpoint), we can interpolate the function with a Quadratic, which gives a better guess of the original integration.

To extend this though, we can of course add more evenly distributed points to the interval and obtain polynomials of higher degree to achieve better approximation. That is how we have the 3/8 Simpson's rule:

\int_{a}^{b} f (x) d x = \frac{1}{8} (1 f (a) + 3 f (\frac{2 a + b}{3}) + 3 f (\frac{a + 2 b}{3}) + f (b)),

and other Newton-Cotez formulae.

Interpolation of Random Points

The above only interests us to a certain degree, as adding points polynomially adds complexity. We would like improve our result by fine-tuning the points.

To make things easier, let's say we integrate on interval $[- 1, 1]$ . This can be done by a simple change of variable. We are looking for $w_{i}$ 's that best approximates:

\int_{- 1}^{1} f (x) d x \approx \sum_{i = 0}^{N} w_{i} f (x_{i}),

Since we have $N$ $w_{i}$ 's to choose from, the degree of freedom of this system is $N$ , we can expect that the approximation is accurate for polynomials with degree less than $N$ .

Actually, we can achieve that by saying "we want the model be accurate for $x^{k}$ as long as $k ＜ N$ ".

\int_{- 1}^{1} x^{k} d x = \sum_{i = 0}^{N} w_{i} x_{i}^{k} (k ＜ N),

or in matrix format

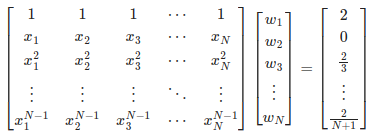matrix format ,

where the coefficient is the well-known Vendermonde matrix. But, can we still improve it?

Roots of Legendre Polynomial

We know that Legendre Polynomial $L_{n} (x)$ is orthogonal to every polynomial that is of degree less than $n$ (because $⟨ x^{k}, L_{n} (x) ⟩ = \sum_{i = 0}^{k} a_{k} ⟨ L_{k} (x), L_{n} (x) ⟩ = 0$ .)

Now if we divide a polynomial $P (x)$ of degree $2 n - 1$ by this $L_{n} (x)$ :

P (x) = Q (x) L_{n} (x) + R (x) .

By synthetic division, $Q (x)$ has a degree less than $2 n - 1 - n$ and $R (x)$ less than $n$ .

\int_{- 1}^{1} P (x) d x = \int_{- 1}^{1} Q (x) L_{n} (x) d x + \int_{- 1}^{1} R (x) d x .

The first term on the right is $⟨ Q (x), L_{n} (x) ⟩ = 0$ , so we can evaluate $\int_{- 1}^{1} P (x) d x$ , the integration of $2 n - 1$ -degree polynomial accurately by evaluating a $n$ -degree polynomial.

The only thing left here is to calculate $R (x_{i})$ . By remainder theorem, we notice that if $L_{n} (x_{i}) = 0$ , then $P (x_{i}) = R (x_{i})$ .

Gaussian Quadrature

The above results summary as following: The integration of any function on $[- 1, 1]$ can be approximated to a polynomial of degree of $2 N - 1$ by calculating the weighted function values $\sum w_{i} f (x_{i})$ , where $x_{i}$ 's are the roots of Legendre polynomial $L_{n} (x)$ and $w_{i}$ 's are obtained by interpolation.

This method is known as Gaussian Quadrature rule, and can be applied to other orthogonal polynomials.

#"hs-maths"